This post will show a way to calculate the approximate mass of the sun. The value can be determined from knowing the time period of the Earth’s orbit around the Sun and assuming the Earth’s orbit is circular (which it very nearly is).
Need to obtain the following from elsewhere:
D = average Sun-Earth distance = 134030000 km (get from solution to one of my previous science posts)
G = universal gravitational constant = 6.673×10^{−11} Nm^2/kg^2 (first lab measurement was made by Cavendish in 1798)
T = average period of the Earth’s orbit = 365 days = 31536000 seconds (count of days from summer solstice to summer solstice or winter solstice to winter solstice or spring equinox to spring equinox or autumn equinox to autumn equinox.)
The following will be calculated:
M = mass of the Sun
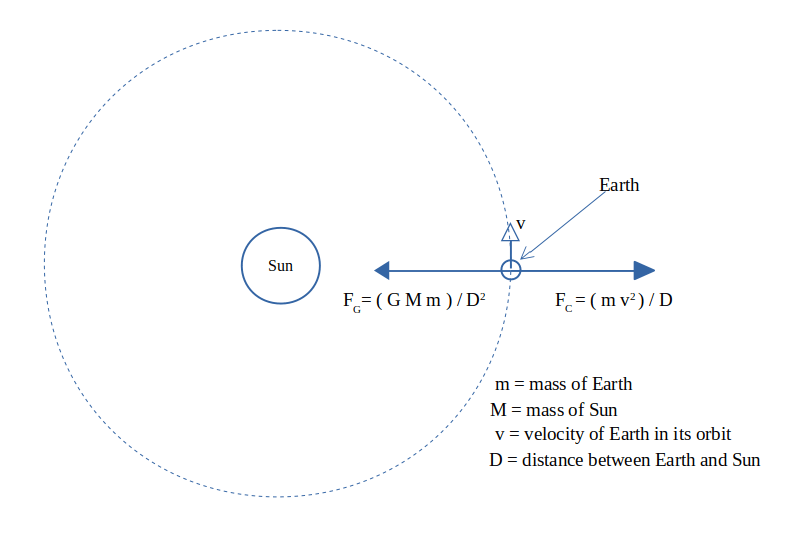
Calculation of the approximate mass of the sun:
For the Earth to be in the circular orbit, the gravitational force between the Sun and the Earth is equal to centripetal force of the Earth about the Sun:
1. Let m be the mass of the Earth.
(G*M*m)/ D^2 = (m*v^2)/D (Note that “m” cancels out of both sides of the equation.)
2. Now solve for M:
M = (v^2*D) / G
3. If T is the period of the orbit of the Earth, then:
v = 2*π*D / T
4. Then insert the expression for v into the equation for M:
M = (4*π^2*D^2*D) / (T^2*G) = (4*π^2*D^3) / (G*T^2)
M = ( 4*(3.142)^2*(134030000 km)^3 ) / ( (6.673×10^{−11} Nm^2/kg^2)*(31536000 s)^2 ) = 1.4323×10^{30} kg
Approximate mass of the Sun = 1.4323×10^{30} kg
Modern value for mass of the Sun: 1.9891×10^{30} kg
Percent difference is: 28%
Sources of error:
The sources of error in this approximation are:
• uncertainty in the value of the universal gravitational constant
• uncertainty in the average Sun-Earth distance
• uncertainty in the Earth’s orbital period
• incorrect assumption that the Earth’s orbit about the Sun is circular. In fact it is very slightly elliptical.
Improving the result:
We can get a substantial improvement in the result if we simply replace the average Sun-Earth distance computed from one of my previous science posts with the modern value of 148090000000 meters:
Approximate mass of the Sun (using modern average Sun-Earth distance) = 1.93197×10^{30} kg
The percent difference from the modern value for mass of Sun is: 2.9%
Since the mass of the Sun cannot be measured either directly or indirectly, it has to be computed. The modern value for the mass of the Sun is calculated from the above equation, but with modern values for G, D, and T. For the value of G, the best estimate is used. Also, the values used for D and T are the best estimates for the Earth. In addition, a check is performed by comparing the result from using the Earth with the results when using planets with very low orbit eccentricities (recall that the above equation assumes the planet’s orbit about the Sun is circular).
Source of modern value for mass of the sun:
The modern values are from the NASA Fact Sheets, located at:
https://nssdc.gsfc.nasa.gov/planetary/factsheet/
The notes on the NASA Fact Sheets state the following:
“Note that the values listed on the fact sheets are not “official” values, there is no single set of agreed upon values. They are based on ongoing research and as such are under study and subject to change at any time.
Every effort has been made to present the most up-to-date information, but care should be exercised when using these values.”

