This post shows an approximate way to calculate the radius of the earth as well as the circumference of the earth. This post uses the method of Eratosthenes.
Eratosthenes (born 276 BC, died 194 BC) of Alexandria, Egypt was the first person to calculate reasonably accurate values for the circumference and radius of the Earth. He was multi-talented, being proficient in astronomy, mathematics, poetry, and geography. He was also the chief librarian of the Library of Alexandra.
One day, at approximately the day of the summer solstice, Eratosthenes happened to be talking to a visitor from Syene (modern day Aswan). The visitor mentioned that every year on this day there are no shadows at noon in Syene. It occurred to Eratosthenes that the Sun must be directly over Syene at noon on the day of the summer solstice. But since the Sun still casts shadows in Alexandria at noon of that day, the Sun must not be directly over Alexandria.
Eratosthenes thought about how to use this information. He used his knowledge of geometry and trigonometry and that fact that the shape of the Earth is that of a sphere to guide him. It seemed to him that it was possible to compute the radius and circumference of the Earth. (Egyptian astronomers knew the Earth is nearly a sphere at least as far back as 500 BC. Also, much of geometry and the means of measuring angles were already known by Eratosthenes’s time.)
After much thought Eratosthenes realized how he could calculate the radius of the Earth. It would be possible using the angle subtended by the Sun between Alexandria and Syene at noon on the day of the summer solstice. Since Alexandria was almost directly north of Syene, Alexandria and Syene would lie approximately on a great circle that crosses the two poles. So at noon Eratosthenes measured the angle between the horizontal length of the Sun’s shadow and the vertical. He found it to be about seven degrees. Then he had someone pace out the distance between Alexandria and Syene using the standard distance measure in use at that time. This turned out to be 5000 stadia or 780 km by our measurements.
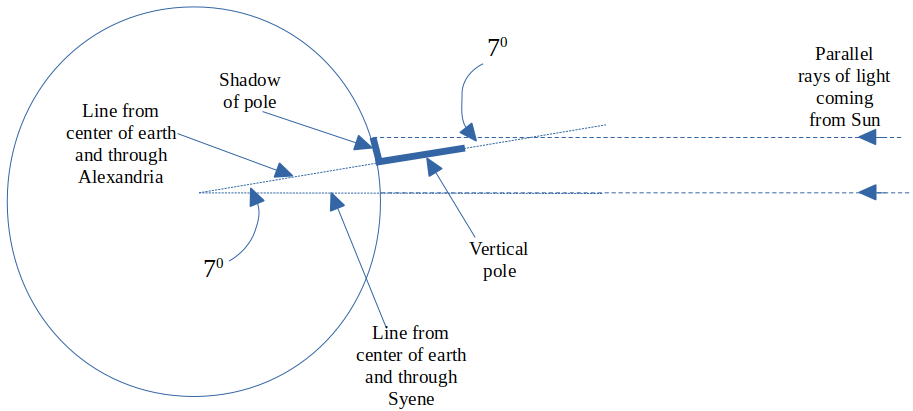
Figure 1: Eratosthenes’s Method for Determining the Radius of the Earth
To compute the radius and circumference of the Earth, the following need to be measured:
D = Distance between Alexandria and Syene = 780 km
ϴ = Angle of shadow cast by pole in Alexandria = 7deg
For the calculations:
Let C represent the circumference of the Earth
Let R represent the radius of the Earth
Calculate the circumference of the earth:
From the ratios: D / ϴ = C / (360 deg)
We plug in the values: (780 km) / (7 deg) = C / (360 deg)
Solving for C: C = (360 deg)*(780 km) / (7 deg) = 40000 km
Therefore, approximate circumference of the Earth = 40,000 km
Modern value for average circumference of the Earth: 40,030 km.
Relative error: < .1%
Calculate the radius of the Earth:
R = C / (2*π) = 40,000 km / (2*π) = 6366 km
Approximate radius of the Earth = 6366 km
Modern value for average radius of the Earth: 6371 km
Relative error: < .1%
Sources of error:
The main sources of error in Eratosthenes’s method arise from the difficulty in accurately measuring the angle of the shadow cast by the pole in Alexandria and the cumulative errors incurred while measuring the distance between Alexandria and Syene. Other errors are due to the Sun not truly being exactly overhead at noon on the day of the summer solstice, and Alexandria and Syene not being precisely at the same longitude. (Eratosthenes was lucky that these two sources of errors were small.) Nevertheless, Eratosthenes’s approach results in a very respectable approximation for the radius and circumference of the Earth.
Source of modern values for circumference and radius of the Earth:
The modern approach computes the Earth’s radius and circumference indirectly from a numerical algorithm for computing the Earth’s gravitational potential. The input consists of ground-based measurements of gravity, satellite-based altimeter radar measurements, satellite-based gravitational radiometer measurements, as well as other data.
The algorithm tries to model these measurements, which depend on the unknown coefficients of the Earth’s gravitational potential. The algorithm tries various values for the coefficients and repeatedly refines them until the it minimizes the differences between the input data and the computed data. Two items that are indirectly produced by this algorithm are the average radius and average circumference of the Earth. This modern approach reveals that the Earth is an oblate spheroid with a polar radius of 6356.14 km and an equatorial radius of 6376.14 km.
Note that these numbers show that the Earth is only mildly oblate. The polar radius differs from the equatorial radius by only 20 km which is a tiny percentage of the Earth’s average radius. However, the difference is of importance in situations that require high precision (examples: geopositioning, inertial guidance systems of ballistic missiles, control of weather and communication satellites, etc.).
The modern values are from the NASA Fact Sheets, located at:
https://nssdc.gsfc.nasa.gov/planetary/factsheet/
The notes on the NASA Fact Sheets state the following:
“Note that the values listed on the fact sheets are not “official” values, there is no single set of agreed upon values. They are based on ongoing research and as such are under study and subject to change at any time.
Every effort has been made to present the most up-to-date information, but care should be exercised when using these values.”