This post will show a way to calculate the approximate distances between the sun and planets. This method requires the following steps:
Step 1: Use Kepler’s third law to determine the approximate distance of each planet from the Sun as a fraction of the Sun-Earth distance. (Kepler’s third law was published sometime between 1609 and 1619.)
Step 2: Use a slight variation of the method of Cassini and Richer to calculate the approximate Earth-Mars distance. (Cassini and Richer used this method in 1672.) (We will also use the radius of the Earth, R, calculated in one of my previous science posts. That is, R = 6370 km.)
Step 3: Use Kepler’s third law again and the results from another of my previous science posts to calculate the approximate distance between the Sun and the planets.
Step 1:
Using the data from detailed planetary observations made by several astronomers over many years, Johannes Kepler’s determined three empirical laws that he published between 1609 and 1619. The third of these laws essentially states that the square of the orbital period of a planet divided by the cube of its distance from the Sun gives the same number regardless of which planet is used in the equation. Thus, for the six planets known at that time, one can write:
(T_{mercury})^2/(D_{mercury})^3 = (T_{venus})^2/(D_{venus})^3
= (T_{earth})^2/(D_{earth})^3
= (T_{mars})^2/(D_{mars})^3
= (T_{jupiter})^2/(D_{jupiter})^3
= (T_{saturn})^2/(D_{saturn})^3
where:
T = orbital period of the planet about the Sun
D = distance of the planet from the Sun
The data Kepler used also included the orbital periods of these six planets. I have added Uranus and Neptune which were not known to Kepler:
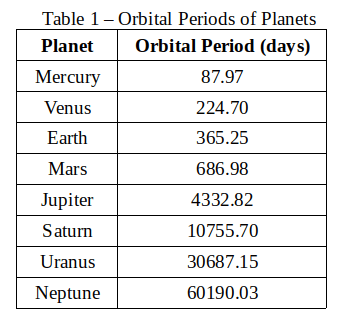
By working with the Earth and Mercury, the distance of Mercury from the Sun could then be determined relative to the Earth’s distance from the Sun.
(T_{mercury})^2/(D_{mercury})^3 = (T_{earth})^2/(D_{earth})^3
D_{mercury} = ( (T_{mercury})^2/(T_{earth})^2 )^{1/3} * D_{earth}
= ( (87.97)^2/(365.26)^2 )^{1/3} * D_{earth}
= 0.3865 * D_{earth}
Repeating this process with the Earth and Venus, then the Earth and Mars, etc, the distance of each planet from the Sun in terms of the Earth’s distance from the Sun can be gotten. Kepler published a table of these fractional distances in 1618.
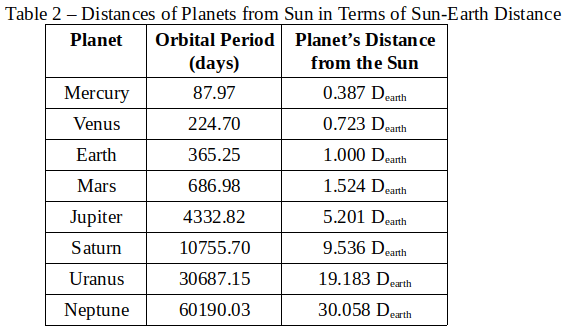
Therefore, if the Sun-Earth distance can be determined, then the distances of the other planets from the Sun can be easily calculated.
Step 2:
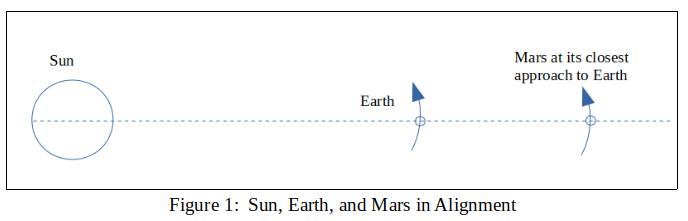
The value of the Sun-Earth distance remained unknown for many years. A few approaches were tried but they gave distances that seemed to the astronomers to be far too low. Then in 1672 Jean Richer and Giovanni Domenico Cassini tried a clever method using parallax when Mars was closest to the Earth (i.e. when the Sun, Earth, and Mars are aligned).
Note: The best source (though vague in places) that I could find that describes this approach is at:
https://www.astronoo.com/en/articles/first-measurement-of-the-earth-sun-distance.html
Cassini and Richer took measurements from two points on the Earth (Paris, France and Cayenne, French Guiana). From these two points they measured the angular location of Mars relative to the “fixed” background stars. Then they used these measurements to compute the angle ϴ. Cassini chose to define the angle ϴ as the angle between Paris and a point located at the Cayenne latitude and Paris longitude. The value Cassini got from his calculations was: ϴ = 14″
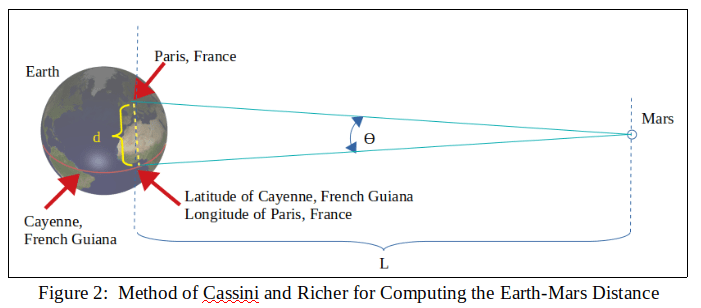
Cassini and Richer calculated the distance “d” from knowledge of the latitude and longitude of Paris and Cayenne and knowledge of the radius of the Earth. The latitudes were easily determined by comparing star observations against star charts. But longitudes were difficult to determine so Cassini resorted to taking averages from several methods. These methods involved historical eclipse data, eclipses of the moons of Jupiter, and observations of the meridian heights of the Sun.
At this point I will deviate from the method of Cassini and Richer. I will use more accurate values for latitude and longitude that I’ve gotten from map data. These values are:
Paris Observatory, Paris, France:
latitude = 48.835880 = 48.835880 * (π/180) radians = 0.8523469 radians
longitude = 2.336560 = 2.336560 * (π/180) radians = 0.04078067 radians
Center of Cayenne, French Guiana:
latitude = 4.927220 = 4.927220 * (π/180) radians = 0.08599621 radians
longitude = -52.314090 = -52.314090 * (π/180) radians = -0.91305312 radians
Next I will convert the latitudes and longitudes of the following points to Cartesian coordinates:
Point 1: The latitude and longitude of the Paris Observatory in Paris, France.
Point 2: The latitude of Cayenne, French Guiana and the longitude of the Paris Observatory in Paris, France.
For Point 1:
From my previous science post we computed the radius of the Earth to be: R = 6370 km.
For Paris: latitude = 0.8523469 radians; longitude = 0.04078067 radians
x1 = R * cos(latitude) * cos(longitude) = 4190.0212877
y1 = R * cos(latitude) * sin(longitude) = 170.96664178
z1 = R * sin(latitude) = 4796.26240067
For Point 2:
From my previous science post we computed the radius of the Earth to be: R = 6370 km.
For Cayenne: latitude = 0.08599621 radians; longitude = -0.91305312 radians
x2 = R * cos(latitude) * cos(longitude) = 6342.17925451
y2 = R * cos(latitude) * sin(longitude) = 258.7817613
z2 = R * sin(latitude) = 547.2068199
Then I can determine the distance “d” between the observers in Paris and Cayenne by calculating the distance between these two points.
d = ( (x2-x1)^2 + (y2-y1^2 + (z2-z1)^2 )^{1/2} = 4763.81871378 km
Since ϴ is a very small angle, it is reasonable to say that “d” is approximately the arc spanned by ϴ. Now the Earth-Mars distance can be calculated from the equation for calculating arc length: d = L * ϴ
(Note that the unit for ϴ needs to be radians, so we need to convert ϴ from degrees to radians.)
L = d / ( (π/180)* (ϴ/3600) ) = 70186000 km
Earth-Mars distance = 70186000 km
Step 3:
Using Kepler’s third law for the Earth and Mars we have:
(T_{mars})^2/(D_{mars})^3 = (T_{earth})^2/(D_{earth})^3
But from step 2 we also have:
D_{mars} = D_{earth} + L
Combining these two equations and solving for D_{earth}, we get:
D_{earth} = ( (T_{earth})^{2/3} / ((T_{mars})^{2/3} – (T_{earth})^{2/3}) ) * L
= ( (365.25)^{2/3} / ((686.95)^{2/3} – (365.25)^{2/3}) ) * 70186000 km
D_{earth} = 134030000 km
The modern value is: 148090000 km
My value differs from the modern value by 9.5%
(Cassini arrived at D_{earth} = 127,891,500 km, which differs from the modern value by 13.5%)
Now in Table 3 we can replace D_{earth} with the value 134030000 km. However, we will instead replace D_{earth} with the modern value 148090000 km.
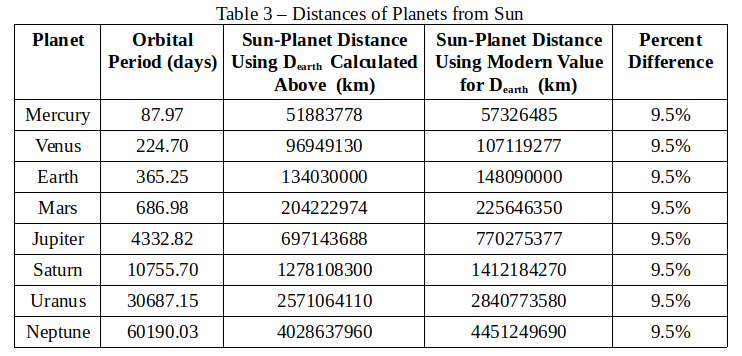
Sources of error:
The sources of error in this approximation are:
• the uncertainty in the measurements of the orbital periods of the planets
• the uncertainties in the angle measurements made by Cassini and Richer
• the uncertainty in the determination of the distance between Paris and Cayenne
An additional source of error is actually in Kepler’s third law. When Newton tried to derive Kepler’s third law he discovered that Kepler’s equation was not quite correct. Kepler had deduced his equation by considering the possible parameters that could affect an orbit and then he used those parameters in trial equations in an attempt to fit the observation data. However the instruments used back when the observation data were gotten had appreciable uncertainty, so Kepler would have easily missed any small effects due to other parameters. Essentially he missed the masses of the planets orbiting the Sun.
Since the mass of any of the planets is significantly less than the mass of the Sun, the error that resulted from Kepler’s approach is not terribly large. These error sources result in a value for the average Sun-Earth distance that is incorrect by approximately 9.5%. Since this value is used in each computation of an average Sun-planet distance, those distances are also incorrect by approximately 9.5%. (Note that using Cassini’s value for the Paris-Cayenne distance will result in larger Sun-planet errors of approximately 12%.)
[Note: We can’t use Newton’s more accurate method here in our computations of the Sun-planets distances because it requires also knowing the masses of the planets. That is, we would have two unknowns in our equation, thus we won’t be able to solve for the Sun-planet distance. Prior to spacecraft missions to the planets, only the masses of the planets with moons were known, but only to a rough approximation. The masses became better known only recently after spacecraft had been sent to orbit the planets so that the masses could be indirectly computed from spacecraft tracking data and the equation for gravity. The mass of the Earth is an exception since the Earth’s mass can be easily computed as shown in one of my previous science posts.]
Source of the modern values for distances between the sun and planets:
The modern values of the Sun-planet distances are obtained in a complex way. The method uses tracking data of spacecraft orbiting a planet as well as astrometric data. The measurement types used are:
• Spacecraft measurements
• Astrometric measurements
Spacecraft measurements consist of Deep Space Network (DSN) radio range and Doppler measurements taken from the DSN ground stations on the Earth. Astrometric measurements consist of values of right ascension and declination which determine the direction to the planet based on its location relative to the background stars.
Once the orbits of the planets about the Sun are determined, the average Sun-planet distances are computed from the orbits.
• The orbit of Mercury is mainly determined from the radio range data for the MESSENGER spacecraft.
• The orbit of Venus is mainly determined from the radio range data for the Venus Express spacecraft.
• The orbit of Mars is mainly determined from the radio range data of the Mars Express (MEX), the Mars Global Surveyor (MGS), the Mars Odyssey (ODY), and the Mars Reconnaissance Orbiter (MRO) spacecraft.
• The orbit of Jupiter is mainly determined from the radio range data for the Juno spacecraft.
• The orbit of Saturn is mainly determined from the radio range data for the Cassini spacecraft.
• The orbits of Uranus and Neptune are mainly determined by astrometry and from the radio range measurements to the Voyager I and Voyager II spacecraft during their “flyby” of Uranus and Neptune.
(See the documentation at: https://ssd.jpl.nasa.gov/planets/eph_export.html)
The modern values are from the NASA Fact Sheets, located at:
https://nssdc.gsfc.nasa.gov/planetary/factsheet/
The notes on the NASA Fact Sheets state the following:
“Note that the values listed on the fact sheets are not “official” values, there is no single set of agreed upon values. They are based on ongoing research and as such are under study and subject to change at any time.
Every effort has been made to present the most up-to-date information, but care should be exercised when using these values.”

Simply a smiling visitant here to share the love (:, btw great design.